ProfileBase¶

Base module that provides essential tools and transformations on airfoils.

`ProfileBase._update_edges`	Private method that identifies and updates the airfoil’s leading and trailing edges.
`ProfileBase.chord_length`	Measure the l2-norm (Euclidean distance) between the leading edge and the trailing edge.
`ProfileBase.compute_camber_line`	Compute the 2D coordinates of the camber line.
`ProfileBase.compute_chord_line`	Compute the 2D coordinates of the chord line.
`ProfileBase.deform_camber_line`	Deform camber line according to a given percentage of change of the maximum camber.
`ProfileBase.interpolate_coordinates`	Interpolate the airfoil coordinates from the given data set of discrete points.
`ProfileBase.max_camber`	Return the magnitude of the airfoil’s maximum camber.
`ProfileBase.max_thickness`	Return the airfoil’s maximum thickness.
`ProfileBase.plot`	Plot the airfoil coordinates.
`ProfileBase.reference_point`	Return the coordinates of the chord’s mid point.
`ProfileBase.reflect`	Reflect the airfoil coordinates about the origin, i.e.
`ProfileBase.rotate`	2D counter clockwise rotation about the origin of the Cartesian
`ProfileBase.scale`	Scale the airfoil coordinates according to a scaling factor.
`ProfileBase.translate`	Translate the airfoil coordinates according to a 2D translation vector.

class ProfileBase[source]

Bases: object

Base sectional profile of the propeller blade.

Each sectional profile is a 2D airfoil that is split into two parts: the upper and lower parts. The coordiates of each part is represented by two arrays corresponding to the X and Y components in the 2D coordinate system. Such coordinates can be either generated using NACA functions, or be inserted directly by the user as custom profiles.

Parameters:

xup_coordinates (numpy.ndarray) – 1D array that contains the X-components of the airfoil upper-half surface. Default value is None
xdown_coordinates (numpy.ndarray) – 1D array that contains the X-components of the airfoil lower-half surface. Default value is None
yup_coordinates (numpy.ndarray) – 1D array that contains the Y-components of the airfoil upper-half surface. Default value is None
ydown_coordinates (numpy.ndarray) – 1D array that contains the Y-components of the airfoil lower-half surface. Default value is None
chord_line (numpy.ndarray) – contains the X and Y coordinates of the straight line joining between the leading and trailing edges. Default value is None
camber_line (numpy.ndarray) – contains the X and Y coordinates of the curve passing through all the mid-points between the upper and lower surfaces of the airfoil. Default value is None
leading_edge (numpy.ndarray) – 2D coordinates of the airfoil’s leading edge. Default values are zeros
trailing_edge (numpy.ndarray) – 2D coordinates of the airfoil’s trailing edge. Default values are zeros

_update_edges()[source]

Private method that identifies and updates the airfoil’s leading and trailing edges.

Given the airfoil coordinates from the leading to the trailing edge, if the trailing edge has a non-zero thickness, then the average value between the upper and lower trailing edges is taken as the true trailing edge, hence both the leading and the trailing edges are always unique.

chord_length

Measure the l2-norm (Euclidean distance) between the leading edge and the trailing edge.

Returns:	chord length
Return type:	float

compute_camber_line(n_interpolated_points=None)[source]

Compute the 2D coordinates of the camber line. Also updates the camber_line class member.

The camber line is defined by the curve passing through all the mid points between the upper surface and the lower surface of the airfoil.

Parameters:	n_interpolated_points (int) – number of points to be used for the equally-spaced sample computations. If None then there is no interpolation, unless the arrays x_up != x_down elementwise which implies that the corresponding y_up and y_down can not be comparable, hence a uniform interpolation is required. Default value is None

We note that a uniform interpolation becomes necessary for the cases when the X-coordinates of the upper and lower surfaces do not correspond to the same vertical sections, since this would imply inaccurate measurements for obtaining the camber line.

compute_chord_line(n_interpolated_points=None)[source]

Compute the 2D coordinates of the chord line. Also updates the chord_line class member.

The chord line is the straight line that joins between the leading edge and the trailing edge. It is simply computed from the equation of a line passing through two points, the LE and TE.

Parameters:	n_interpolated_points (int) – number of points to be used for the equally-spaced sample computations. If None then there is no interpolation, unless the arrays x_up != x_down elementwise which implies that the corresponding y_up and y_down can not be comparable, hence a uniform interpolation is required. Default value is None

deform_camber_line(percent_change, n_interpolated_points=None)[source]

Deform camber line according to a given percentage of change of the maximum camber. Also reconstructs the deformed airfoil’s coordinates.

The percentage of change is defined as follows:

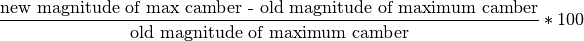
$\frac{\text{new magnitude of max camber - old magnitude of maximum camber}}{\text{old magnitude of maximum camber}} * 100$

A positive percentage means the new camber is larger than the max camber value, while a negative percentage indicates the new value is smaller.

We note that the method works only for airfoils in the reference position, i.e. chord line lies on the X-axis and the foil is not rotated, since the measurements are based on the Y-values of the airfoil coordinates, hence any measurements or scalings will be inaccurate for the foils not in their reference position.

Parameters:

percent_change (float) – percentage of change of the maximum camber. Default value is None
interpolate (bool) – if True, the interpolated coordinates are used to compute the camber line and foil’s thickness, otherwise the original discrete coordinates are used. Default value is False.
n_interpolated_points (int) – number of points to be used for the equally-spaced sample computations. If None then there is no interpolation, unless the arrays x_up != x_down elementwise which implies that the corresponding y_up and y_down can not be comparable, hence a uniform interpolation is required. Default value is None

interpolate_coordinates(num=500, radius=1.0)[source]

Interpolate the airfoil coordinates from the given data set of discrete points.

The interpolation applies the Radial Basis Function (RBF) method, to construct approximations of the two functions that correspond to the airfoil upper half and lower half coordinates. The RBF implementation is present in RBF ndinterpolator.

References:

Buhmann, Martin D. (2003), Radial Basis Functions: Theory and Implementations. http://www.cs.bham.ac.uk/~jxb/NN/l12.pdf https://www.cc.gatech.edu/~isbell/tutorials/rbf-intro.pdf

Parameters:	num (int) – number of interpolated points. Default value is 500 radius (float) – range of the cut-off radius necessary for the RBF interpolation. Default value is 1.0. It is quite necessary to adjust the value properly so as to ensure a smooth interpolation
Returns:	interpolation points for the airfoil upper half X-component, interpolation points for the airfoil lower half X-component, interpolation points for the airfoil upper half Y-component, interpolation points for the airfoil lower half Y-component
Return type:	numpy.ndarray, numpy.ndarray, numpy.ndarray, numpy.ndarray
Raises:	TypeError – if num is not of type int ValueError – if num is not positive, or if radius is not positive

max_camber(n_interpolated_points=500)[source]

Return the magnitude of the airfoil’s maximum camber.

Camber is defined as the distance between the chord line and the mean camber line, and is measured along the line perpendicular to the chord line.

Parameters:	interpolate (bool) – if True, the interpolated coordinates are used to measure the camber; otherwise, the original discrete coordinates are used. Default value is False n_interpolated_points (int) – number of points to be used for the equally-spaced sample computations. If None then there is no interpolation, unless the arrays x_up != x_down elementwise which implies that the corresponding y_up and y_down can not be comparable, hence a uniform interpolation is required. Default value is None
Returns:	maximum camber
Return type:	float

max_thickness(n_interpolated_points=None)[source]

Return the airfoil’s maximum thickness.

Thickness is defined as the distnace between the upper and lower surfaces of the airfoil, and can be measured in two different ways:

American convention: measures along the line perpendicular to the mean camber line.

British convention: measures along the line perpendicular to the chord line.

In this implementation, the british convention is used to evaluate the maximum thickness.

References:

Phillips, Warren F. (2010). Mechanics of Flight (2nd ed.). Wiley & Sons. p. 27. ISBN 978-0-470-53975-0.

Bertin, John J.; Cummings, Russel M. (2009). Pearson Prentice Hall, ed. Aerodynamics for Engineers (5th ed.). p. 199. ISBN 978-0-13-227268-1.

Parameters:	interpolate (bool) – if True, the interpolated coordinates are used to measure the thickness; otherwise, the original discrete coordinates are used. Default value is False n_interpolated_points (int) – number of points to be used for the equally-spaced sample computations. If None then there is no interpolation, unless the arrays x_up != x_down elementwise which implies that the corresponding y_up and y_down can not be comparable, hence a uniform interpolation is required. Default value is None
Returns:	maximum thickness
Return type:	float

plot(profile=True, chord_line=False, camber_line=False, ref_point=False, outfile=None)[source]

Plot the airfoil coordinates.

Parameters:

profile (bool) – if True, then plot the profile coordinates. Default value is True
chord_line (bool) – if True, then plot the chord line. Default value is False
camber_line (bool) – if True, then plot the camber line. Default value is False
ref_point (bool) – if True, then scatter plot the reference point. Default value is False
outfile (str) – outfile name. If a string is provided then the plot is saved with that name, otherwise the plot is not saved. Default value is None

reference_point

Return the coordinates of the chord’s mid point.

Returns:	reference point in 2D
Return type:	numpy.ndarray

reflect()[source]: Reflect the airfoil coordinates about the origin, i.e. a mirror transformation is performed about both the X-axis and the Y-axis.

rotate(rad_angle=None, deg_angle=None)[source]

2D counter clockwise rotation about the origin of the Cartesian coordinate system.

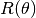The rotation matrix, $R(\theta)$ , is used to perform rotation in the 2D Euclidean space about the origin, which is – by default – the leading edge.

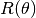$R(\theta)$ is defined by: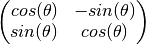

$\left(\begin{matrix} cos (\theta) & - sin (\theta) \\ sin (\theta) & cos (\theta) \end{matrix}\right)$

Given the coordinates of point $P$ such that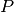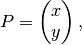

$P = \left(\begin{matrix} x \\ y \end{matrix}\right),$

Then, the rotated coordinates will be:

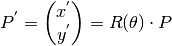
$P^{'} = \left(\begin{matrix} x^{'} \\ y^{'} \end{matrix}\right) = R (\theta) \cdot P$

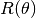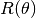If a standard right-handed Cartesian coordinate system is used, with the X-axis to the right and the Y-axis up, the rotation $R (\theta)$ is counterclockwise. If a left-handed Cartesian coordinate system is used, with X-axis directed to the right and Y-axis directed down, $R (\theta)$ is clockwise.

Parameters:	rad_angle (float) – angle in radians. Default value is None deg_angle (float) – angle in degrees. Default value is None
Raises:	ValueError – if both rad_angle and deg_angle are inserted, or if neither is inserted

scale(factor)[source]

Scale the airfoil coordinates according to a scaling factor.

In order to apply the scaling without affecting the position of the reference point, the method translates the airfoil by its refernce point to be centered in the origin, then the scaling is applied, and finally the airfoil is translated back by its reference point to the initial position.

Parameters:	factor (float) – the scaling factor

translate(translation)[source]

Translate the airfoil coordinates according to a 2D translation vector.

Parameters:	translation (array_like) – the translation vector in 2D