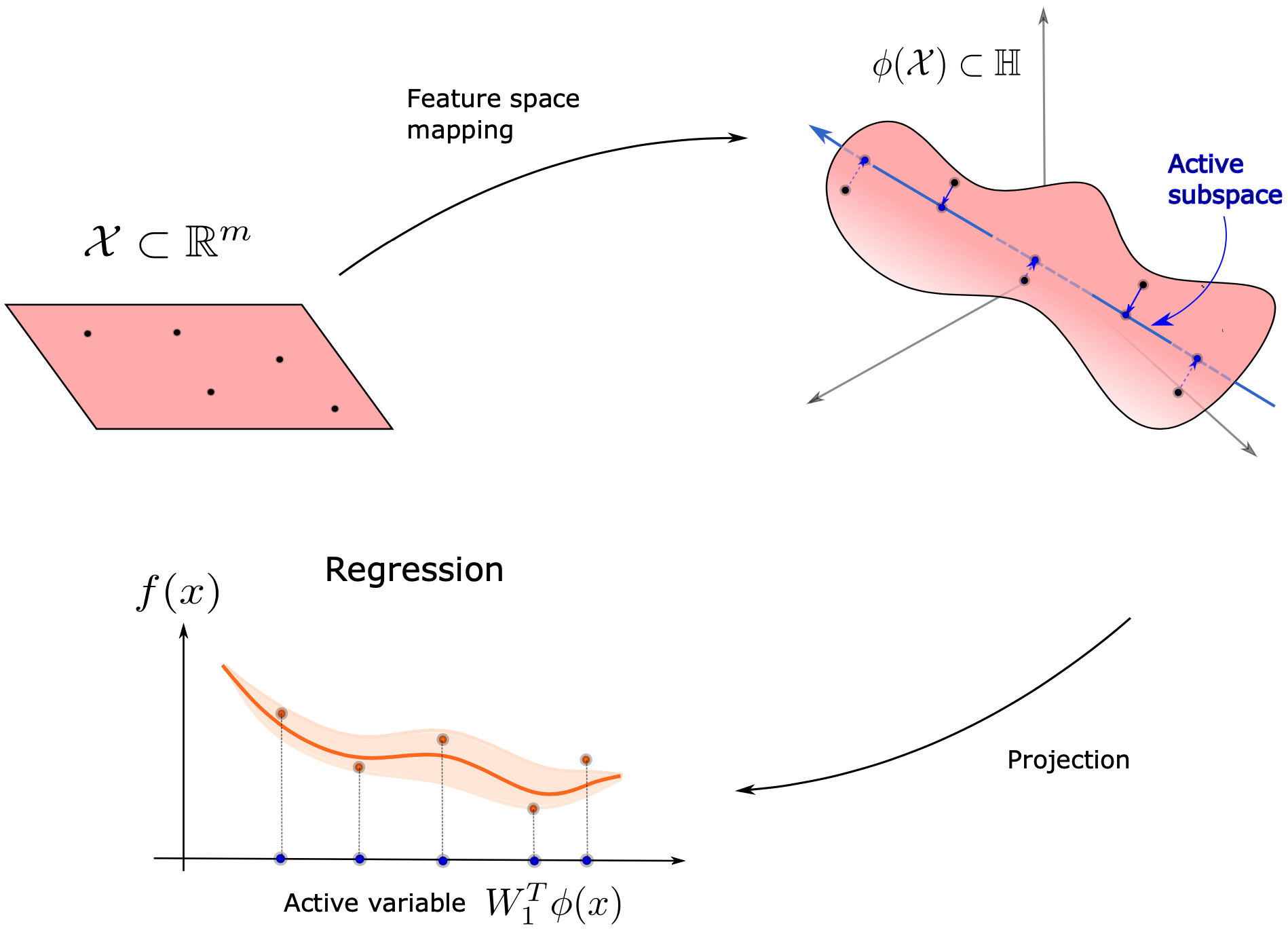
In order to extend the methodology to cases which don't have an Active Subspace, we can consider searching for a kernel-based Active Subspace.
As is common practice in Machine Learning to project the inputs from $\chi\subset\mathbb{R}^{m}$ to a Reproducing Kernel Hilbert Space (RKHS), the inputs are immersed with a feature space map $\phi$ into a supposedly infinite-dimensional Hilbert space $\phi(\chi)\subset\mathbb{H}$. Then the model function of interest factorizes over this feature map $\phi$ and a new model function $\bar{f}$ with domain the feature space
$$ f:\chi\subset\mathbb{R}^{m}\rightarrow\mathbb{R},\quad \phi:\chi\subset\mathbb{R}^{m}\rightarrow\mathbb{H}\approx\mathbb{R}^{D},\quad\bar{f}:\phi(\chi)\subset\mathbb{H}\rightarrow\mathbb{R}\\ $$$$ f = \bar{f}\circ\phi $$the RKHS $\mathbb{H}$ is approximated with a discrete feature space $\mathbb{R}^{D}$.
Searching for a kernel-based Active Subspace then reduces to finding an Active Subspace of the new model function $\bar{f}:\chi\subset\mathbb{H}\rightarrow\mathbb{R}$. In this tutorial we will consider the design of one-dimensional response functions with Gaussian process regression. A scheme of the procedure is shown below

To look more in to the details of the procedure see Kernel-based Active Subspaces with application to CFD parametric problems using Discontinuous Galerkin method. The feature map we adopt was introduced in Gaussian Process Modeling and Supervised Dimensionality Reduction Algorithms via Stiefel Manifold Learning.
import autograd.numpy as np
from autograd import elementwise_grad as egrad
import matplotlib.pyplot as plt
from functools import partial
import GPy
from athena.active import ActiveSubspaces
from athena.kas import KernelActiveSubspaces
from athena.feature_map import FeatureMap, rff_map, rff_jac
from athena.projection_factory import ProjectionFactory
from athena.utils import Normalizer, CrossValidation, average_rrmse
from numpy_functions import radial
np.random.seed(42)
# global parameters
n_samples = 800 # this is the number of data points to use for the tuning of kas
N = 500 # this is the number of test samples to use
input_dim = 2
# set the dimension of the discrete feature space (D in the introduction)
n_features = 1000
def sample_in_out(input_dim, n_samples):
#input ranges
lb = np.array(-3 * np.ones(input_dim))
ub = np.array(3 * np.ones(input_dim))
#input normalization
XX = np.random.uniform(lb, ub, (n_samples, input_dim))
nor = Normalizer(lb, ub)
x = nor.fit_transform(XX)
#output values (f) and gradients (df)
func = partial(radial, normalizer=nor, generatrix=lambda x: np.cos(x))
f = func(x)
df = egrad(func)(x)
return x, f, df
Some samples (xx, f, df) will be used for the tuning phase of the kernel-based active subspaces proceure, the remaining (y, t, dt) represents the test dataset.
xx, f, df = sample_in_out(input_dim, n_samples)
y, t, dt = sample_in_out(input_dim, N)
An active subspace is searched for, but due to the radial symmetry of the model there is no preferred direction of variation. The same result could be obtained changing the generatrix of the model. These are cases where linear active subspaces are not present and other methods should be taken in consideration.
#AS
ss = ActiveSubspaces(1)
ss.fit(gradients=dt, outputs=t, inputs=y)
ss.plot_eigenvalues(figsize=(6,4))
ss.plot_sufficient_summary(y, t, figsize=(6,4))
Define the feature map and pass it to the KernelActiveSubspaces class. The feature map is defined as
$$ \phi(\mathbf{x})=\sqrt{\frac{2}{D}}\,\sigma_f\,\cos(W\mathbf{x}+\mathbf{b}),\\ \cos(W\mathbf{x}+\mathbf{b}):=\frac{1}{\sqrt{D}}(\cos(W[1, :] \cdot \mathbf{x} +b_1),\dots, \cos(W[D, :] \cdot \mathbf{x} +b_D))^T $$where $\sigma_f$ cooresponds to the empirical variance of the model, $W\in \mathcal{M}(D\times m,\mathbb{R})$ is the projection matrix whose rows are sampled from a probability distribution on $\mathbb{R}^m$ and $\mathbf{b}\in \mathbb{R}^D$ is a bias term whose components are sampled independently and uniformly in the interval $[0, 2\pi]$.
# number of parameters of the spectral distribution associated to the feature map
# this is the number of parameters to tune after
n_params = 1
# sample the bias term
b = np.random.uniform(0, 2 * np.pi, n_features)
The list of implemented distributions to chose from is the following, the number of parameters to tune for each distribution is reported in the documentation.
ProjectionFactory.projections
['beta', 'cauchy', 'dirichlet', 'laplace', 'multivariate_normal', 'normal', 'uniform']
# define the feature map
fm = FeatureMap(distr='laplace',
bias=b,
input_dim=input_dim,
n_features=n_features,
params=np.zeros(n_params),
sigma_f=f.var())
# instantiate a KernelActiveSubspaces object with associated feature map
kss = KernelActiveSubspaces(feature_map=fm, dim=1, n_features=n_features)
The feature map hyperparameters are to be tuned. Different methods are available, see the documentation. In this tutorial we will use Bayesian stochastic optimization.
# number of folds for the cross-validation algorithm
folds = 3
verbose = True
# Skip if bias and projection matrix are loaded
csv = CrossValidation(inputs=xx,
outputs=f.reshape(-1, 1),
gradients=df.reshape(n_samples, 1, input_dim),
folds=folds,
subspace=kss)
best = fm.tune_pr_matrix(func=average_rrmse,
bounds=[slice(-2, 0., 0.2) for i in range(n_params)],
fn_args={'csv':csv, 'verbose':verbose},
method='bso',
maxiter=5,
save_file=False)
print('The lowest rrmse is {:.3f}%'.format(best[0]*100))
################################################################################ params [0.54987828] mean 0.5806036102762929, std 0.10557747169663108 params [0.54987828] mean 0.6508088337502892, std 0.258403783743379 params [0.54987828] mean 0.5069359497235307, std 0.09170534906677469 params [0.54987828] mean 0.8635941179089066, std 0.1961446264598243 ################################################################################ params [0.63303763] mean 0.7716216067211062, std 0.16253579937856896 params [0.63303763] mean 0.4363267355882392, std 0.03816486064204355 params [0.63303763] mean 0.5060488192912277, std 0.10575725753696222 params [0.63303763] mean 0.28767888162252037, std 0.04720140191709448 params [0.63303763] mean 0.5410136102749092, std 0.08078987768134094 ################################################################################ params [0.04487257] mean 1.0027281038779663, std 0.0014114084641444664 ################################################################################ params [0.01527761] mean 1.0006766975337171, std 0.0007903166463334343 ################################################################################ params [0.02632185] mean 1.0079474661484877, std 0.0050811175188999 ################################################################################ params [0.73153169] mean 1.0011729712197917, std 0.0014860539187824704 ################################################################################ params [0.60876305] mean 0.9878218849767153, std 0.01783448985892262 ################################################################################ params [0.63410858] mean 0.9873291014883088, std 0.022116121930394826 ################################################################################ params [0.63308181] mean 1.0005712907971323, std 0.0007047386631580656 ################################################################################ params [0.47263103] mean 0.9936583636821269, std 0.009511940097498308 The lowest rrmse is 28.768%
#W = np.load('opt_pr_matrix.npy')
#b = np.load('bias.npy')
#fm._pr_matrix = W
#fm.bias = b
kss.fit(gradients=dt.reshape(N, 1, input_dim),
outputs=t,
inputs=y)
kss.plot_eigenvalues(n_evals=5, figsize=(6,4))
kss.plot_sufficient_summary(xx, f, figsize=(6,4))
# comparison with Nonlinear Level-set Learning explained in detail in tutorial 07
from athena.nll import NonlinearLevelSet
import torch
# create NonlinearLevelSet object, eventually passing an optimizer of choice
nll = NonlinearLevelSet(n_layers=10,
active_dim=1,
lr=0.01,
epochs=1000,
dh=0.25,
optimizer=torch.optim.Adam)
# convert to pytorch tensors
x_torch = torch.as_tensor(xx, dtype=torch.double)
df_torch = torch.as_tensor(df, dtype=torch.double)
# train RevNet
nll.train(inputs=x_torch,
gradients=df_torch,
interactive=False)
epoch = 0, loss = 7.532548972955653 epoch = 10, loss = 7.221680266861894 epoch = 20, loss = 6.643592148573998 epoch = 30, loss = 6.24253642188315 epoch = 40, loss = 6.075985928347147 epoch = 50, loss = 5.9537479695453985 epoch = 60, loss = 5.8628279384482385 epoch = 70, loss = 5.845114644336895 epoch = 80, loss = 5.835431386654003 epoch = 90, loss = 5.830508028305733 epoch = 100, loss = 5.827308701073581 epoch = 110, loss = 5.824416541472429 epoch = 120, loss = 5.821889732655846 epoch = 130, loss = 5.819171229026848 epoch = 140, loss = 5.816033053439709 epoch = 150, loss = 5.811848882827806 epoch = 160, loss = 5.805241360822049 epoch = 170, loss = 5.7923747549712346 epoch = 180, loss = 5.762065173938508 epoch = 190, loss = 5.688055808002115 epoch = 200, loss = 5.571285061230882 epoch = 210, loss = 5.563880224857506 epoch = 220, loss = 5.543796546106483 epoch = 230, loss = 5.538031414804469 epoch = 240, loss = 5.535185033113964 epoch = 250, loss = 5.533332289181305 epoch = 260, loss = 5.532587489204041 epoch = 270, loss = 5.532057783857496 epoch = 280, loss = 5.531638363376278 epoch = 290, loss = 5.531268982856506 epoch = 300, loss = 5.530915371046731 epoch = 310, loss = 5.530580639574407 epoch = 320, loss = 5.530262078113562 epoch = 330, loss = 5.5299576649163455 epoch = 340, loss = 5.529666320852156 epoch = 350, loss = 5.529386745345333 epoch = 360, loss = 5.529117858349119 epoch = 370, loss = 5.528858709559586 epoch = 380, loss = 5.528608349135078 epoch = 390, loss = 5.528365802869438 epoch = 400, loss = 5.528130070891185 epoch = 410, loss = 5.527900122898406 epoch = 420, loss = 5.527674901251468 epoch = 430, loss = 5.527453322478689 epoch = 440, loss = 5.527234279955423 epoch = 450, loss = 5.527016648946539 epoch = 460, loss = 5.526799291686672 epoch = 470, loss = 5.526581062586568 epoch = 480, loss = 5.5263608124343575 epoch = 490, loss = 5.526137390939807 epoch = 500, loss = 5.525909647105348 epoch = 510, loss = 5.52567642685884 epoch = 520, loss = 5.525436567811005 epoch = 530, loss = 5.525188891587697 epoch = 540, loss = 5.524932195023223 epoch = 550, loss = 5.524665242526729 epoch = 560, loss = 5.524386762880344 epoch = 570, loss = 5.52409545428638 epoch = 580, loss = 5.523790001337072 epoch = 590, loss = 5.523469106462441 epoch = 600, loss = 5.523131536130243 epoch = 610, loss = 5.522776178648663 epoch = 620, loss = 5.522402106057409 epoch = 630, loss = 5.522008627817818 epoch = 640, loss = 5.521595319831193 epoch = 650, loss = 5.521162010335759 epoch = 660, loss = 5.520708706671569 epoch = 670, loss = 5.520235455698472 epoch = 680, loss = 5.519742145538583 epoch = 690, loss = 5.51922827233139 epoch = 700, loss = 5.518692702635283 epoch = 710, loss = 5.5181334490403104 epoch = 720, loss = 5.517547440958744 epoch = 730, loss = 5.516930227006406 epoch = 740, loss = 5.516275511212924 epoch = 750, loss = 5.515574413873817 epoch = 760, loss = 5.514814344842364 epoch = 770, loss = 5.5139773487695525 epoch = 780, loss = 5.5130376965386585 epoch = 790, loss = 5.51195833353722 epoch = 800, loss = 5.510685512902382 epoch = 810, loss = 5.509140414094771 epoch = 820, loss = 5.507205440533864 epoch = 830, loss = 5.504700394034741 epoch = 840, loss = 5.501338118018588 epoch = 850, loss = 5.496639517337872 epoch = 860, loss = 5.489799979315683 epoch = 870, loss = 5.479748125307383 epoch = 880, loss = 5.46652045173461 epoch = 890, loss = 5.453305225267302 epoch = 900, loss = 5.443000146630938 epoch = 910, loss = 5.435389483692386 epoch = 920, loss = 5.429188859742997 epoch = 930, loss = 5.423144195953234 epoch = 940, loss = 5.416715958963219 epoch = 950, loss = 5.409938251952806 epoch = 960, loss = 5.402960728929154 epoch = 970, loss = 5.39594203618684 epoch = 980, loss = 5.389094660484148 epoch = 990, loss = 5.382651715329154 epoch = 999, loss = 5.377359102673039
# loss history plot and sufficient summary plot
nll.plot_loss(figsize=(6, 4))
nll.plot_sufficient_summary(x_torch, f, figsize=(6, 4))